Question

A student randomly guesses on 10 true or false questions use the bionomial model to find the probability that the student gets 7 out of the 10 questions right

Answer 1

Option A: 11.8%

Explanation:

The total number of question n=10

The probability of getting true is
`p=(1)/(2)`

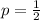
The probability of getting false is
`q=(1)/(2)`

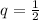
It is given that the student gets 7 out of 10 questions right, the,
`x=7`

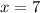
Using binomial distribution formula,

`P(x)=\left[(n !)/(x !(n-x) !)\right] p^(x) q^(n-x)`

Substituting the values, we get,

`\begin{aligned}P(7) &=\left[(10 !)/(7 !(10-7) !)\right]\left((1)/(2)\right)^(7)\left((1)/(2)\right)^(3) \\&=\left[(10 !)/(7 ! 3 !)\right]\left((1)/(2)\right)^(7+3)\end{aligned}`

Solving, we get,

`P(7)=(15)/(128)`

`P(7)=0.118`

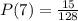
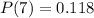
To find the probability, multiply it by 100, we get,

`0.118*100=11.8`%

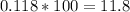Thus, the correct answer is 11.8%