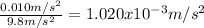Answer:
The centripetal acceleration as a multiple of
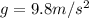 is
is
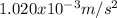
Step-by-step explanation:
The centripetal acceleration is defined as:
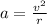 (1)
(1)
Where v is the velocity and r is the radius
Since the person is standing in the Earth surfaces, their velocity will be the same of the Earth. That one can be determined by means of the orbital velocity:
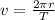 (2)
(2)
Where r is the radius and T is the period.
For this case the person is standing at a latitude
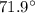 . Remember that the latitude is given from the equator. The configuration of this system is shown in the image below.
. Remember that the latitude is given from the equator. The configuration of this system is shown in the image below.
It is necessary to use the radius at the latitude given. That radius can be found by means of trigonometric.
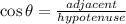
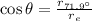 (3)
(3)
Where
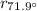 is the radius at the latitude of
is the radius at the latitude of
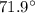 and
and
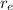 is the radius at the equator (
is the radius at the equator (
 ).
).
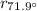 can be isolated from equation 3:
can be isolated from equation 3:
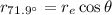 (4)
(4)
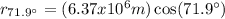
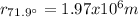
Then, equation 2 can be used
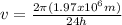
Notice that the period is the time that the Earth takes to give a complete revolution (24 hours), this period will be expressed in seconds for a better representation of the velocity.
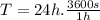 ⇒
⇒
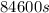
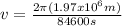
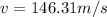
Finally, equation 1 can be used:

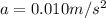
Hence, the centripetal acceleration is
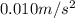
To given the centripetal acceleration as a multiple of
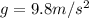 it is gotten:
it is gotten: