Question

A bag containing originally 60 kg of flour is lifted through a vertical distance of 9 m. While it is being lifted, flour is leaking from the bag at such rate that the number of pounds lost is proportional to the square root of the distance traversed. If the total loss of flour is 12 kg find the amount of work done in lifting the bag.

Answer 1

The total work done is 5997.6 J

Solution:

As per the question:

Mass of the bag, m = 60 kg

Vertical distance, h = 9 m

Mass lost, m' = 12 kg

To calculate the amount of work done:

Lost mass is proportional to the square root of the distance covered while lifting:

m' ∝
`√(h)`

m' =
`K√(9)`

where

K = proportionality constant

12 = 3K

K = 4

Mass of the floor containing bag at a height h:

`m(h) = 60 - k√(h)`

Work done is given by:

`W = \int_(0)^(h)m(h)gdh`

`W = \int_(0)^(9)(60 - k√(h))gdh`

`W = g([60h]_(0)^(9) + 4* (2)/(3)[h^{(3)/(2)}]_(0)^(9))`

`W = 9.8* ([60* 9 - 0] + (8)/(3)[9^{(3)/(2)} - 0^{(3)/(2)}])`

`W = 9.8* (540 + (8)/(3)* 27) = 5997.6\ J = 5.9976\ kJ`

Answer 2

The amount of work done in lifting the bag is -20109.6 N-m

Step-by-step explanation:

Given that,

Mass of bag = 60 kg

Distance = 9 m

Loss of mass = 12 kg

The number of pounds lost is proportional to the square root of the distance traversed

Mass of the bag containing flour at height is

`m(y)=60-k√(y)`

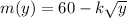
Put the value into the formula

`60-k√(y)=12`

`k=144`

We need to calculate the work done

Using formula of work done

`W=\int_(0)^(9){m(y)gdy}`

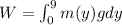
Put the value into the formula

`W=\int_(0)^(9){(60-k√(y))gdy}`

`W=((60y-(2k)/(3)* y^{(3)/(2)}})_(0)^(9))*9.8`

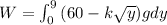
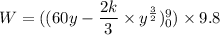
Put the value of y

`W=(60*9-(2*144)/(3)* 9^{(3)/(2)})*9.8`

`W=-20109.6\ N-m`

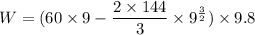
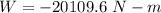
Hence, The amount of work done in lifting the bag is -20109.6 N-m