Answer:
0.6547 or 65.47%
Explanation:
One minute equals 1/60 of an hour, the mean number of occurrences in that interval is:
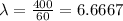
The poisson distribution is described by the following equation:
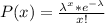
The probability that more than 5 vehicles will arrive is:
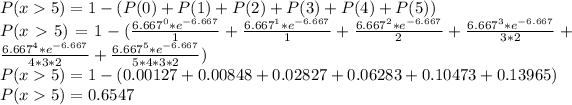
The probability that more than five vehicles will arrive in a one-minute interval is 0.6547 or 65.47%.