Question

A tin can has a volume of 1100 cm³ and a mass of 80 g. Approximately how many grams of lead shot can it carry without sinking in water? The density of lead is 11.4 g/cm³.

Answer 1

1020g

Step-by-step explanation:

Volume of can=
`1100cm^3=1100* 10^(-6)m^3`

`1cm^3=10^(-6)m^3`

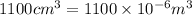
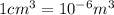
Mass of can=80g=
`(80)/(1000)=0.08kg`

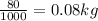
1Kg=1000g

Density of lead=
`11.4g/cm^3=11.4* 10^(3)=11400kg/m^3`

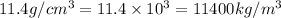
By using
`1g/cm^3=10^3kg/m^3`

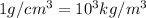
We have to find the mass of lead which shot can it carry without sinking in water.

Before sinking the can and lead inside it they are floating in the water.

Buoyancy force =
`F_b=Weight of can+weight of lead`

`\rho_wV_cg=m_cg+m_lg`

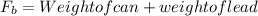
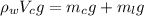
Where
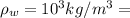`\rho_w=10^3kg/m^3=`Density of water

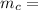`m_c=`Mass of can

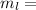`m_l=`Mass of lead

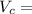`V_c=`Volume of can

Substitute the values then we get

`1000* 1100* 10^(-6)=0.08+m_l`

`1.1-0.08=m_l`

`m_l=1.02 kg=1.02* 1000=1020g`

`1 kg=1000g`

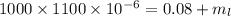
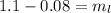
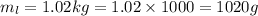
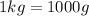
Hence, 1020 grams of lead shot can it carry without sinking water.