8 : 1 is the ratio of the areas of these similar rectangles
Solution:
Given that, rectangle has an area of 25 square feet
A similar rectangle has an area of 200 square feet
To find: Ratio of the areas of these similar rectangles
Ratio of the areas of these similar rectangles can be found dividing the area of rectangles
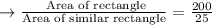
Reduce the fraction to lowest term
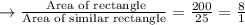
In ratios we get,
Area of rectangle : Area of similar rectangle = 8 : 1
Thus 8 : 1 is the ratio of the areas of these similar rectangles