Question

ΔEFG is located at E (0, 0), F (−7, 4), and G (0, 8). Which statement correctly classifies ΔEFG?

ΔEFG is a scalene triangle.
ΔEFG is an isosceles triangle.
ΔEFG is an equilateral triangle.
ΔEFG is a right triangle.

Answer 1

B

Explanation:

Answer 2

ΔEFG is an isosceles triangle.

Explanation:

Given:

E (0, 0),

F (−7, 4),

G (0, 8)

ΔEFG

Solution:

Distance formula

Distance d =
`\sqrt{(x_2-x_1)^2 +( y_2-y_1)^2`

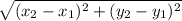
Step 1: Finding the length of EF

By using distance formula,

`EF = √((-7 - 0)^2 + (4-0)^2)`

`EF = √((49) + (16))`

`EF = √((49) + (16))\\EF = √(65)\\`

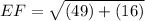
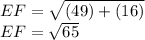
Step 2: Finding the length of FG

By using distance formula,

`FG = √((0-(-7))^2+(8-4)^2)\\FG = √((7)^2 +(4)^2)\\FG = √(49 +16)\\FG = √(65)`

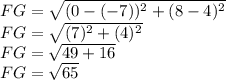
Step 2: Finding the length of GE

`GE= √((0-0)^2 + (0-8)^2)\\\\GE =√((-8)^2)\\GE = √(64)\\GE = 8`

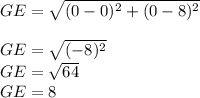
Thus we could see that the sides EF = FG

So it is a isosceles triangle.