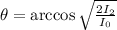Answer: The unpolarized light's intensity is reduced by the factor of two when it passes through the polaroid and becomes linearly polarized in the plane of the Polaroid. When the polarized light passes through the polaroid with the plane of polarization at an angle
 with respect to the polarization plane of the incoming light, the light's intensity is reduced by the factor of
with respect to the polarization plane of the incoming light, the light's intensity is reduced by the factor of
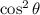 (this is the Law of Malus).
(this is the Law of Malus).
Explanation: Let us say we have a beam of unpolarized light of intensity
 that passes through two parallel Polaroid discs with the angle of
that passes through two parallel Polaroid discs with the angle of
 between their planes of polarization. We are asked to find
between their planes of polarization. We are asked to find
 such that the intensity of the outgoing beam is
such that the intensity of the outgoing beam is
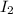 . To solve this we follow the steps below:
. To solve this we follow the steps below:
Step 1. It is known that when the unpolarized light passes through a polaroid its intensity is reduced by the factor of two, meaning that the intensity of the beam passing through the first polaroid is
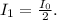
This beam also becomes polarized in the plane of the first polaroid.
Step 2. Now the polarized beam hits the surface of the second polaroid whose polarization plane is at an angle
 with respect to the plane of the polarization of the beam. After passing through the polaroid, the beam remains polarized but in the plane of the second polaroid and its intensity is reduced, according to the Law of Malus, by the factor of
with respect to the plane of the polarization of the beam. After passing through the polaroid, the beam remains polarized but in the plane of the second polaroid and its intensity is reduced, according to the Law of Malus, by the factor of
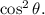 This yields
This yields
 . Substituting from the previous step we get
. Substituting from the previous step we get
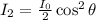
yielding
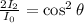
and finally,