Question

A 400 kg satellite orbits the moon at a height of 2000 km above the moon at a speed of 946 m/s. The speed of a 800 kg satellite orbiting the moon at 2000 km above the moon is:

Answer 1

To solve this problem we will apply the concepts related to the balance of Forces, in this case the centripetal force of the body must be equal to the gravitational force exerted by the moon on it.

The gravitational force is given by the function

`F_g = (GmM)/(r^2)`

Here

G = Gravitational Universal constant

M = Mass of the planet

m = Mass of the satellite

r = Radius(orbit)

Now the centripetal force is given as

`F_c =(mv^2)/(r)`

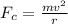
Here

m = mass of satellite

v = Velocity of satellite

r = Radius (orbit)

Since there must be balance for the satellite to remain in the orbit

`F_c = F_g`

`(mv^2)/(r) = (GmM)/(r^2)`

`v^2= (GM)/(r)`

`v=\sqrt{(GM)/(r)}`

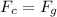
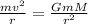
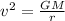
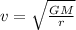
The velocity depends on the mass of the planet and the orbit, and not on the mass, so if the orbit is maintained, the velocity will be the same: 946m/s