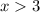Answer:
The correct option is C. 3
Therefore the value of x in the solution set of

is
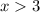
Explanation:
Given:

To Find:
x = ?
Solution:
 .......Given:
.......Given:
Step 1 : Add '6' on Both the side we get
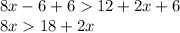
Step 2 : Subtract '2x' from Both the side we get
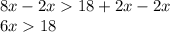
Step 3 : Dividing by '6 on Both the side we get
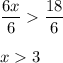
Therefore the value of x in the solution set of

is