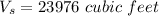Answer:
Option 3 is correct.
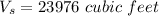
Explanation:
Given:
The dimension of the large box.
Length = 40 ft,width = 24, height = 18
The dimension of the smaller box.
Box 1 ⇒ Length = 30 ft, width = 18 ft, height = 6 ft
Box 2 ⇒ Length = 30 ft, width = 12 ft height = 6 ft
Box 3 ⇒ Length = 18 ft, width = 12 ft, height = 6 ft
We need to find the volume of the solid.
Solution:
First we find the volume of the all boxes by using below formula.
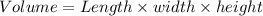
Volume of the large box.
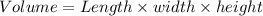
So, the volume of the large box.
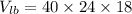

Volume of the smaller box(box 1).
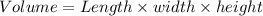
So, the volume of the large box.
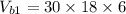

Volume of the smaller box(box 2).
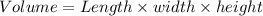
So, the volume of the large box.
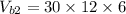
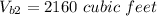
Volume of the smaller box(box 3).
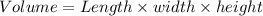
So, the volume of the large box.
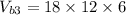
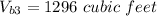
We know that the volume of the solid is equal to sum of the all boxes.
Volume of the solid


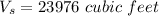
Therefore, the volume of the solid