Answer: (0.05256, 0.10744) .
Explanation:
We know that the confidence interval for population proportion is given by :-
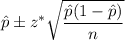 (1)
(1)
, where
 = Sample proportion
= Sample proportion
n= Sample size
z* = Critical z-value.
Let p be the population proportion of all medical students who plan to work in a rural community.
As per given , we have
n= 375
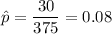
Critical z-value for 95% confidence interval = 1.96
Put all values in (1) , we get
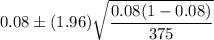
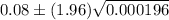
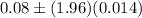
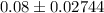
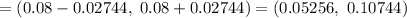
Hence, the 95% confidence interval for the true population proportion of all medical students who plan to work in a rural community is (0.05256, 0.10744) .