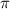Question

Use the fundamental identities and appropriate algebraic operations to simplify the following expression. (18 +tan x) (18-tan x)+ sec 2x Complete the following statement The lowest point on the graph of y = cos x, 0sxs2x, occurs when x-

Answer 1

a)
`\left(18+\tan \left(x\right)\right)\left(18-\tan \left(x\right)\right)+\sec ^2\left(x\right)=325`

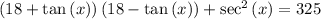
b) The lowest point of
`y=\cos \left(x\right)`,
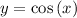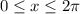`0\leq x\leq 2\pi` is when x =
`\pi`

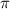
Explanation:

a) To simplify the expression
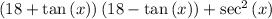`\left(18+\tan \left(x\right)\right)\left(18-\tan \left(x\right)\right)+\sec ^2\left(x\right)` you must:

Apply Difference of Two Squares Formula:
`\left(a+b\right)\left(a-b\right)=a^2-b^2`

`a=18,\:b=\tan \left(x\right)`

`\left(18+\tan \left(x\right)\right)\left(18-\tan \left(x\right)\right)=18^2-\tan ^2\left(x\right)=324-\tan ^2\left(x\right)`

`324-\tan ^2\left(x\right)+\sec ^2\left(x\right)`

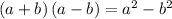
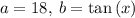
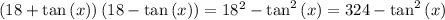
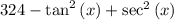
Apply the Pythagorean Identity
`1+\tan ^2\left(x\right)=\sec ^2\left(x\right)`

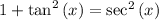
From the Pythagorean Identity, we know that
`1=-\tan ^2\left(x\right)+\sec ^2\left(x\right)`

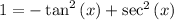
Therefore,

`324[-\tan ^2\left(x\right)+\sec ^2\left(x\right))]\\324[+1]\\325`

b) According with the below graph, the lowest point of
`y=\cos \left(x\right)`,
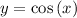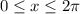`0\leq x\leq 2\pi` is when x =
`\pi`