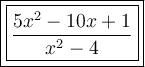Answer:
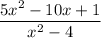
Explanation:
Given rational expression:
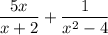
To add two fractions, they must share a common denominator.
In this case, we start by factoring the denominator of the second fraction using the difference of two squares formula, a² - b² = (a + b)(a - b):
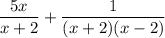
To ensure both fractions have the same denominator, we multiply the numerator and denominator of the first fraction by (x - 2):
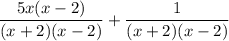
Now that both fractions share the same denominator, we can combine them by adding their numerators:
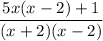
Finally, simplify the numerator and denominator:
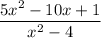
Therefore, the simplified rational expression is: