Question

A gas within a piston–cylinder assembly undergoes a

thermodynamic cycle consisting of three processes:
Process 1–2: Compression with pV= constant, from p1=1 bar,V1=2m3 to V2=0.2m3,U2−U1=100kJProcess 2–3: Constant volume to p3=p1Process 3–1: Constant-pressure and adiabatic process.

There are no significant changes in kinetic or potential
energy. Determine the net work of the cycle, in kJ, and the
heat transfer for process 2–3, in kJ. Is this a power cycle or
a refrigeration cycle? Explain.

Answer 1

`W_(net)= -280.5 kJ`

`Q_(23)= 80.0 kJ`

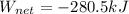
Step-by-step explanation:

The net work of the cycle is the sum of works in each process.

For the first process 1-2: Let's apply the work definition.

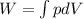`W=\int pdV` (1)

Now, we need the pressure. We know that pV=C, where C is a constant. Then
`p_(1)V_(1)=10^(5)2=2*10^(5) [J]`

So
`p=(2*10^(5))/(V)`

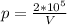
Let's put p in (1):

`W_(12)=\int (2*10^(5))/(V)dV=2*10^(5)\int (1)/(V)dV`

`W_(12)=2*10^(5)(ln(V_(2))-ln(V_(1)))=2*10^(5)(ln(0.2)-ln(2))=-460.5 kJ`

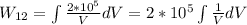
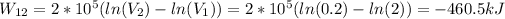
Using the first law of thermodynamics we can find Q.

`Q_(12)-W=\Delta U`

`Q_(12)=W+\Delta U=-460.5 + 100= -360.5 kJ`

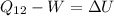
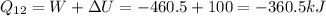
Second process 2-3

In this case, we have a constant volume, so the work done here is 0.

`W_(23)=0`

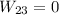
Third process 3-1

`W_(31)=\int pdV=p\int dV=p(V_(2)-V_(1))`

`W_(31)=10^(5)(2-0.2)=180 kJ`

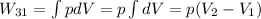
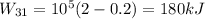
Finally, the net work is:

`W_(net)=W_(12)+W_(23)+W_(31)= -280.5 kJ`

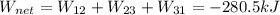
By the conservation of energy:

`(Q_(12)+Q_(23)+Q_(31))-(W_(net))=\Delta E=0`

Because there is no change in total energy.

So:

`Q_(23)=W_(net)-Q_(12)= 80.0 kJ`

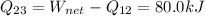
It is a refrigerator because the net work is negative, it means it consumes energy.

I hope it helps you!