Question

The National Survey of Family Growth conducted by the Centers for Disease Control gathers information on family life, marriage and divorce, pregnancy, infertility, use of contraception, and men's and women's health. One of the variables collected on this survey is the age at first marriage. The histogram below shows the distribution of ages at first marriage of 5,534 randomly sampled women between 2006 and 2010. The average age at first marriage among these women is 23.5 with a standard deviation of 4.7 (approximate values from NSFG, 2010). Estimate the average age at first marriage of women using a 95% confidence interval, and interpret this interval in context. Discuss any relevant assumptions.

Answer 1

Answer with explanation:

The confidence interval for population mean is given by :-

`\overline{x}\pmz^*(\sigma)/(√(n))`

, where n= Sample size

`\overline{x}`= Sample mean

`\sigma`= Standard deviation

z* = Critical z-value.

Let
`\mu` be the average age at first marriage of women.

As per given ,we have

n= 5,534 ,

`\overline{x}=23.5`

Sample standard deviation : s= 4.7

Since n is extremely very large so we assume that this scenario follows a normal distribution , and thus we can use z-test .

So ,
`\sigma\approx4.7`

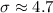
Critical value of 95% confidence level : z=1.96

Put all values in formula , we get

`23.5\pm(1.96)(4.7)/(√(5534))`

`23.5\pm(1.96)(4.7)/(74.39086)`

`23.5\pm(1.96)0.06318`

`23.5\pm0.1238328`

`=(23.5-0.1238328,\ 23.5+ 0.1238328)`

`=(23.3761672,\ 23.6238328)\approx(23.38,\ 23.62)`

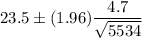
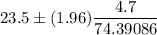
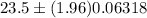
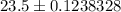
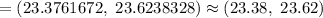
Hence , our 95% confidence interval =(23.38, 23.62)

Interpretation : The National Survey of Family Growth can be 95% sure that the true population mean age at first marriage of women lies in (23.38, 23.62) .