Question

a)If it takes 0.20 min to decompose 15% of a 0.300 M solution of nitrosyl chloride,what is k(the rate constant)?the decomposition of nitrosyl chloride is a second order reaction:NOCl(g)--->NO(g)+1/2Cl2(g)b)Calculate the activation energy?When the temperature increases from 15C to 25C for a certain reaction, its rate constant doubles. Calculate the activation energy, Ea+ (remember: with R=8.31 J/mol.K, Ea must be expressed in J/mol)

Answer 1

a) k = 0.0417 M⁻¹.s⁻¹

b) Ea = 49.4 kJ/mol

Step-by-step explanation:

a) If the decomposition reaction is a second-order reaction, the rate law is:

rate = k*[NOCl]²

The rate is how much the concentration decays per second (M/s), thus, if its initially 0.300 M and it decays 15%, the final concentrations 85% of 0.300, which is 0.255 M. The time needed for that is 0.20 min = 12 s, so:

rate = (0.300 - 0.255)/12

rate = 0.00375 M/s

Thus, the rate constant is:

0.00375 = k*(0.300)²

0.09k = 0.00375

k = 0.0417 M⁻¹.s⁻¹

b) By the Arrhenius equation, the constant k is related to the activation energy as:

k =
`A*e^{(-Ea)/(RT)`

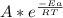
Where A is a constant, R is the gas constant (8.31 J/mol.K) and T is the temperature. If we apply ln in the equation:

ln(k) = ln(A) - Ea/RT

Thus, for T1 = 15°C (288 K), k = k1, and for T = 25°C (298 K), k = k2, knowing that Ea and A are independent of the temperature:

ln(k1) = ln(A) - Ea/RT1

ln(k2) = ln(A) - Ea/RT2

ln(k1) - ln(k2) = ln(A) - ln(A) - Ea/RT1 + Ea/RT2

ln(k1/k2) = (Ea/R) * (1/T2 - 1/T1)

If the rate constant doubles, k2 = 2k1

ln (1/2) = (Ea/8.31) * (1/298 - 1/288)

-0.6932 = (Ea/8.31)*(-1.1652x10⁻⁴)

1.402x10⁻⁵Ea = 0.6932

Ea = 49438.84 J/mol

Ea = 49.4 kJ/mol