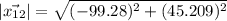Question

From the top of a bridge that is 50 m high, two boats can be seen anchored in a marina. One boat is anchored in the direction S20°W, and its angle of depression is 40°. The other boat is anchored in the direction S60°E, and its angle of depression is 30°. Determine the distance between the two boat

Answer 1

Step-by-step explanation:

Given

height of bridge is
`=50\ m`

First Boat is at an angle of
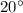`20^(\circ)`w.r.t to x axis

Second boat is at an angle of
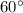`60^(\circ)` w.r.t to x axis

from Diagram

In triangle ABO

`\tan (40)=(h)/(r_1)`

`r_1=(h)/(\tan 40)=59.58\ m`

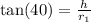
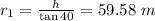
In triangle ACO

`r_2=(h)/(\tan 30)=86.602\ m`

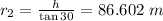
where
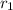`r_1` and
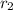`r_2` are the distance of boat from origin O

Position vector of boat 1 w.r.t origin is

`\vec{x_1}=59.58\left ( -\cos (20)\hat{i}-\sin (20)\hat{j}\right )`

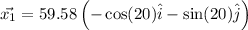
Position vector of boat 2 w.r.t origin is

`\vec{x_2}=86.602\left ( \cos (60)\hat{i}-\sin (60)\hat{j}\right )`

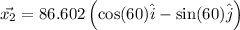
Position of
`\vec{x_1} w.r.t to \vec{x_2}`

`\vec{x_(12)}=59.58\left ( -\cos (20)\hat{i}-\sin (20)\hat{j}\right )-86.602\left ( \cos (60)\hat{i}-\sin (60)\hat{j}\right )`

`\vec{x_(12)}=-99.28\hat{i}+45.209\hat{j}`

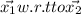
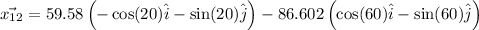
Distance between them is
`|\vec{x_(12)}|=√((-99.28)^2+(45.209)^2)`

`|\vec{x_(12)}|=109.089\ m`