Answer:
Option d) is correct
That is x equals plus or minus start fraction 11 over two end fraction
Explanation:
Given quadratic equation is
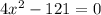
To write the given quadratic equation by using a difference-of-squares factoring method:
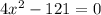
The above equation can be written as
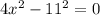
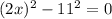
The above equation is in the form of difference-of-squares
Therefore the given quadratic equation can be written in the form of difference-of-squares
by factoring method is
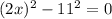
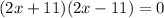 (which is in the form
(which is in the form
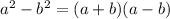 )
)
2x+11=0 or 2x-11=0
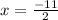 or
or

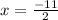 or
or
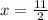
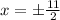
Therefore option d) is correct
That is x equals plus or minus start fraction 11 over two end fraction