Question

5. The measure of an intercepted arc is 86, and the measure of the inscribed angle creating the intercepted arc is 3x +

4. What is the value of x?

A. 30
B. 27 1/3
C. 56
D. 13

Answer 1

13 is your answer

Explanation:

Answer 2

Th correct option is D. 13

Therefore the value of x is 13.

Explanation:

Given:

measure of an intercepted arc = 86°

Center Angle = 86°

measure of the inscribed angle creating the intercepted arc= (3x+4)°

Angle Inscribed in arc = (3x+4)°

To Find:

value of x = ?

Solution:

Inscribed Angle Theorem:

The inscribed angle theorem states that an angle θ inscribed in a circle is half of the central angle 2θ that subtends the same arc on the circle.

`\textrm{Angle Inscribed in arc}=(1)/(2)\textrm{Center Angle}`

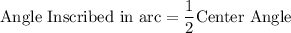
Substituting the values we get

`3x+4=(1)/(2)86=43\\\\3x=39\\\\x=(39)/(3)=13\\\\x=13`

Therefore the value of x is 13.