Question

Find the three angles of the triangle with the given vertices: P(1,1,1), ????(1,−3,2), and ????(−3,2,5).

Answer 1

The three angles of the triangle are 90, 35.67 and 54.33 degrees.

Explanation:

One way to find the angles of the triangle with vertices (1, 1, 1), (1, -3, 2), (-3, 2, 5) is using the definition of the dot product of two vectors, defined as:

a . b = |a| |b| cosФ [1]

Where |a| and |b| are the norms of vectors a and b, and cosФ is the cosine of the angle between either vector a and b.

If a = [
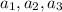`\\ a_(1), a_(2), a_(3)` ] and b = [
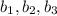`\\ b_(1), b_(2), b_(3)`], then the dot product is simply a number (not a vector) obtained from:

a . b =
`\\ a_(1)*b_(1) + a_(2)*b_(2) + a_(3)*b_(3)`

The norm of a vector (its length) is, for instance, |a| =
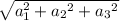`\\ \sqrt{{a_(1)^2 + {a_(2)}^2 + {a_(3)}^2}`, for a vector in
`\\ R^(3)`.

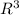Having all that into account, we can determine the angles of the triangle for each vertex using equation [1] and solving it for Ф.

Angle of the triangle for vertex in (1, 1, 1)

The vectors which form an angle from this vertex are the result of subtracting the vertex (1, 1, 1) to any of the remaining points (1, -3, 2) and (-3, 2, 5):

v(1, 1, 1) - v(1, -3, 2) =
`\\ (1 - 1, 1 - (-3), 1 - 2) = (0, 1 + 3, -1) = (0, 4, -1)`

v(1, 1, 1) - v(-3, 2, 5) =
`\\ (1 - (-3), 1 - 2, 1 - 5) = (1 + 3, -1, -4) = (4, -1, -4)`

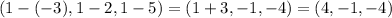
The dot product for these vectors is:

[0, 4, -1] . [4, -1, -4] = [0 * 4 + 4 * -1 + -1 * -4] = 0 - 4 + 4 = 0

The norm for each vector is:

|(0, 4, -1)| =
`\\ √(0^2 + 4^2 + -1^2) = √(0 + 16 + 1) = √(17)`

|(4, -1, -4)| =
`\\ √(4^2 + -1^2 + -4^2) = √(16 + 1 + 16) = √(33)`

So

a . b = |a| |b| cosФ

`\\ 0 = √(17) * √(33) * cos{\theta}`

`\\ (0)/(√(17) * √(33)) = cos{\theta}`

`\\ cos^(-1){0}} = cos^(-1)(cos{\theta})`

`\\ 90 = \theta`

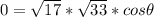
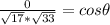
In vertex (1, 1, 1) the angle of the triangle is 90 degrees. We have here a right triangle.

We have to follow the same procedure for finding the vectors for angles in vertices (1, -3, 2) and (-3, 2, 5), or better, after finding one of the previous angles, we find the remaining angle subtracting the sum of two angles from 180 degrees to finally obtaining the three angles in question.

Therefore, the other angles are 35.67 degrees and 180 - (90 + 35.67) = 180 - 125.67 = 54.33 degrees.