Question

Statement A: Area of a rectangle with measured length = 2.536 m and width = 1.4 m.

Statement B: Area of a rectangle with measured length = 2.536 m and width = 1.41 m.
Since you are not told specific numbers of significant figures to round to, you must use the rules for multiplying numbers while respecting significant figures. If you need a reminder, consult the hint.
Determine the correct relationship between the statements.

Answer 1

Statement A is greater than Statement B

Step-by-step explanation:

Statement A

The area A of a rectangle is a product of length and with hence

`A = l * b`

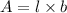
Taking l as 2.536 and b as 1.4 then

`\begin{array}{c}\\A = 2.536\,{\mathop{\rm m}\\olimits} * 1.4\,{\mathop{\rm m}\\olimits} \\\\ = 3.5504\,{\mathop{\rm m}\\olimits} \\\end{array}`

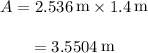
Since 1.4 is the least significant number in the product, with 1 decimal place, so we express our area also to 1 decimal place hence we obtain 3.6

Statement B

The area A of a rectangle is also a product of length and width hence

`A = l * b`

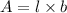
Substitute 2.536 for l and 1.41 for b

`\begin{array}{c}\\A = 2.536\,{\mathop{\rm m}\\olimits} * 1.41\,{\mathop{\rm m}\\olimits} \\\\ = 3.57576\,{\mathop{\rm m}\\olimits} \\\end{array}`

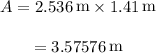
Here, the least significant figure within the product is 1.41 with 3 significant numbers or 2 decimal places so the answer also must be expressed to 3 significant figures which is 3.58

Now comparing 3.6 to 3.58, it's clear that 3.6 is greater than 3.58 so statement A is greater than statement B

Hence, Statement A is greater than Statement B