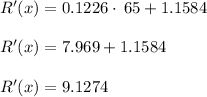Answer:
The marginal-revenue equation is
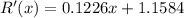 .
.
The marginal revenue for the production of 200,000,000 bushels is
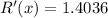 .
.
The marginal revenue for the production of 650,000,000 bushels is
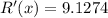 .
.
Explanation:
The derivative
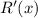 of the revenue function is called the marginal revenue function and is the rate of change of revenue with respect to the number of units sold.
of the revenue function is called the marginal revenue function and is the rate of change of revenue with respect to the number of units sold.
We know the revenue function,
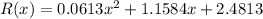 . Therefore, the marginal revenue function is
. Therefore, the marginal revenue function is
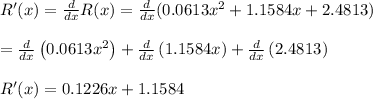
To find the marginal revenue for the production of:
200,000,000 bushels we use x = 2, since x is in units of hundreds of million of dollars.
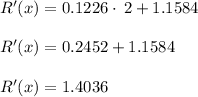
650,000,000 bushels we use x = 65, since x is in units of hundreds of million of dollars.