Question

An ideal gas is compressed at constant pressure p=1500 Pa from a volume Vi=0.4 m3 to Vf=0.25 m3. At the same time, heat is transferred out of the gas into the surroundings. If the intenal energy of the gas is unchanged before and after the compression, how much heat was transferred from the gas to the surroundings?

A. 150 J
B. 225 J
C. 1500 J
D. 0.15J

Answer 1

To solve this problem we will apply the first law of thermodynamics and we will make a balance between the heat transferred, its internal energy and the total work. Recall that for gases the definition of work can be expressed in terms of its pressure and volume. Let's start

`dQ = dU +dW`

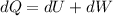
Here,

dU = Internal Energy

dW = Work

But internal energy is unchanged, then

`dQ = dW`

`dQ = PdV`

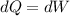
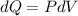
Where

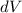`dV`= Change in Volume

P = Pressure

Finally, the expression of the heat transferred can be expressed in terms of pressure and volume, so it would end up becoming

`dQ = p(v_i-v_f)`

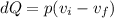
Replacing,

`dQ = (1500)(0.4-0.25)`

`dQ = 225J`

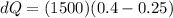
Therefore the correct answer is B.