Question

A thin, uniformly charged insulating rod has a linear charge density λ = 3 nC/m and lies along the x axis from x = 1m to x = 3m.

A) Find the electric potential at point A that has the coordinates (0,4).
B) Find the electric field at that location.

Answer 1

A)
`V_A = 11.93~V`

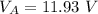
B) The vector definition of E-field is

`\vec{E} = -1.13\^x + 2.41\^y`

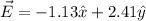
where magnitude is E = 2.66 N/m.

Step-by-step explanation:

The potential of a uniformly charged rod can be found by the method of integration. We will first choose an infinitesimal part on the rod. We will compute the potential of this part at point A. Then we will integrate this potential over the entire rod.

We will use the following formula for electric potential:

`V = (1)/(4\pi \epsilon_0)(Q)/(r)`

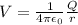
Let us choose the infinitesimal part a distance 'x' from the origin. Then the distance between this point and point A is

`r = √(x^2+4^2)`

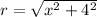
The infinitesimal length is 'dx', and the potential of this length is dV. Let's apply the formula:

`dV = (1)/(4\pi\epsilon_0)(\lambda dx)/(√(x^2 + 4^2))`

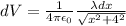
Here, the charge Q is equal to the charge density multiplied by the length. Q = λdx

Now we have to integrate this infinitesimal potential over the rod:

`V = \int\limits^3_1 {dV} \, dx = (1)/(4\pi \epsilon_0)\int\limits^3_1 {(\lambda)/(√(x^2 + 16)) \, dx`

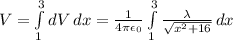
By using an integral table, this can be calculated:

`V = (3* 10^(-9))/(4\pi\epsilon_0)\ln(|√(x^2+16)+x|)\left \{ {{x=3} \atop {x=1}} \right. \\V = 11.93~V`

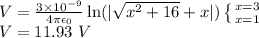
B) The electric field can be found by a similar approach, but a different formula:

`\vec{E} = (1)/(4\pi \epsilon_0)(Q)/(r^2)\^r`

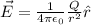
Let's apply this formula to the infinitesimal part we have chosen.

`dE_x = (1)/(4\pi\epsilon_0)(\lambda dx)/(x^2 + 4^2)\cos(\theta)\\dE_y = (1)/(4\pi\epsilon_0)(\lambda dx)/(x^2 + 4^2)\sin(\theta)`

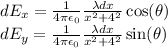
By the geometry sine and cosine terms can be found:

`\sin(\theta) = (4)/(√(x^2+16))\\\cos(\theta) = (x)/(√(x^2 + 16))`

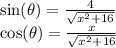
The x- and y-components of the E-field can be found separately by integrating the infinitesimal parts over the entire rod.

`E_x = \int\limits^3_1 {dE_x} \, dx = (\lambda)/(4\pi\epsilon_0)\int\limits^3_1 {(x)/((x^2+16)^(3/2))} \, dx  = 1.13(-\^x)\\E_y = \int\limits^3_1 {dE_y} \, dx = (4\lambda)/(4\pi\epsilon_0)\int\limits^3_1 {(1)/((x^2+16)^(3/2))} \, dx  = 2.41(\^y)`

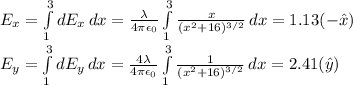
So, the final E-field is

`\vec{E} = -1.13\^x + 2.41\^y`

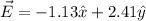
The magnitude of the E-field is

E = 2.66 N/m