Question

An 18% alcohol solution is mixed with a 45% alcohol solution to produce 12 ounces of a 36% alcohol solution. How many ounces of the 18% solution and the 45% solution must be used?

Answer 1

The ounces of the 18% solution is 4 and the ounces of the 45% solution is 8

Explanation:

Let

x ---> ounces of the 18% solution

y ---> ounces of the 45% solution

we know that

The number of ounces of the 18% solution plus the number of ounces of the 45% solution must be equal to 12 ounces

so

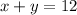`x+y=12` ----> equation A

The number of ounces of the 18% solution multiplied by 0.18 (percentage in decimal form) plus the number of ounces of the 45% solution multiplied by 0.45 (percentage in decimal form), must be equal to 12 ounces multiplied by 0.36 (percentage in decimal form)

so

`0.18x+0.45y=0.36(12)`

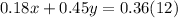
`0.18x+0.45y=4.32` -----> equation B

Solve the system of equations by graphing

Remember that the solution of the system is the intersection point both graphs

using a graphing tool

The solution is the point (4,8)

see the attached figure

therefore

The ounces of the 18% solution is 4 and the ounces of the 45% solution is 8