Question

Find the solutions to the following linear-quadratic systems algebraically. Select the order pair that is one of the correct solutions from among the choices below.

y = -x² -x + 2
y = 2x + 2

(1, 0)
(3, 4)
(2, 0)
(-3, -4)

Answer 1

(-3, -4)

Explanation:

we have

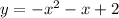`y=-x^(2) -x+2` ----> equation A

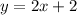`y=2x+2` ----> equation B

equate equation A and equation B

`-x^(2) -x+2=2x+2`

`-x^(2) -x+2-2x-2=0`

`-x^(2) -3x=0`

`x(x+3)=0`

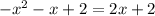
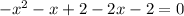
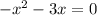
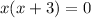
The solutions of the quadratic equation are x=0 and x=-3

Find the values of y

For x=0

`y=2(0)+2=2`

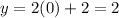
For x=-3

`y=2(-3)+2=-4`

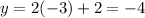
therefore

The solutions of the system are the points (0,2) and (-3,-4)