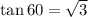Answer:
See explanation and attachment
Explanation:
SOH CAH TOA is a mnemonic.
SOH means

CAH means
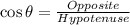
TOA means
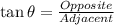
Given an angle and a side of a right angle triangle, you can use the appropriate ratio to find the missing side.
For instance, find x in the diagram in the attachment.
In this case the best ratio to use is TOA.
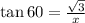
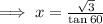
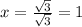
All the other ratio also follow the same pattern
NB: Your calculator in degree should give