Answer:
f(-3)=6 is the greatest value in the range of
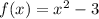 for the domain (-3,0,1,2)
for the domain (-3,0,1,2)
Explanation:
Given that the function f is defined for range by
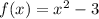 for the domain (-3,0,1,2)
for the domain (-3,0,1,2)
To find the greatest value in the range of
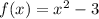 for the domain (-3,0,1,2):
for the domain (-3,0,1,2):
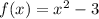 for the domain (-3,0,1,2)
for the domain (-3,0,1,2)
That is put x=-3 in the given function
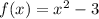 we get
we get

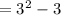
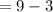

Therefore f(-3)=6
put x=0 in the given function
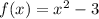 we get
we get



Therefore f(0)=-3
put x=1 in the given function
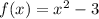 we get
we get
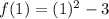
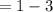

Therefore f(1)=-2
put x=-3 in the given function
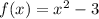 we get
we get

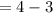
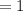
Therefore f(2)=1
Comparing the values of f(-3)=6,f(0)=-3,f(1)=-2,and f(2)=1 to find the greatest value in the range of f(x) = x^2 - 3 for the domain (-3,0,1,2) we get
Therefore f(-3)=6 is the greatest value in the range of
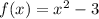 for the domain (-3,0,1,2)
for the domain (-3,0,1,2)