Question

A kite is flying above the ground

at the end of a 100 feet of string.
If the angle of elevation of the
kite is 65°, how high above the
ground is the kite flying?

Answer 1

109 feet D

Explanation:

Answer 2

The height of the kite above the ground is 90.63 feet.

Explanation:

The angle of elevation of the kite is (θ) 65°.

The distance between the kite and its end is (hypotenuse)100 feet.

To find the height (x) of the kite flying above the ground.

we know that sin(θ) =
`(height)/(hypotenuse)`.

sin 65°=
`(x)/(100) .`

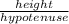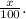
sin 65° = 0.90631.

0.90631 ×100=x.

90.63=x.

∴The height of the kite above the ground is 90.63 feet.