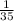Question

In a class of 777, there are 444 students who play soccer. If the teacher chooses 333 students, what is the probability that none of the three of them play soccer?

Answer 1

1/35

Explanation:

khan

Answer 2

`(1)/(35)`

Explanation:

Given:

Total number of students in a class = 7

Number of students who play soccer = 4

Number of students who don't play soccer = 3

Now, number of ways of choosing 3 students out of 7 students is given by their combination.

So, number of ways of choosing 3 students (S)=
`_(3)^(7)\textrm{C}=(7!)/(3!* 4!)=(7* 6** 5* 4!)/(3* 2* 4!)=35`

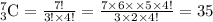
Now, number of choosing 3 students who don't play soccer out of 3 students is given by their combination and is given as:

N =
`_(3)^(3)\textrm{C}=1`

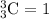
Therefore, the probability that none of the three of them play soccer is given as:

`P(None\ play\ soccer)=(N)/(S)\\\\P(None\ play\ soccer)=(1)/(35)`

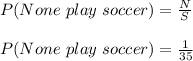
Therefore, the the probability that none of the three of them play soccer is
`(1)/(35)`