Question

Raise to the power:
(a^3n−1)^(2n+1)

Answer 1

The simplified expression for given expression is
`a^(6n^2+n-1)`

Explanation:

Given:

`(a^(3n-1))^(2n+1)`

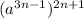
We need to simplify the given equation:

Solution:

`(a^(3n-1))^(2n+1)`

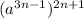
Now By using law of indices which states that;

`(x^m)^n = x^(mn)`

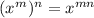
So Applying the same we get;

`a^((3n-1)(2n+1))`

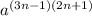
Now applying distributive property we get;

`a^(6n^2+3n-2n-1)\\\\a^(6n^2+n-1)`

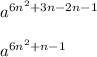
Hence The simplified expression for given expression is
`a^(6n^2+n-1)`