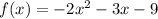Question

Use a system of linear equations to find the quadratic function

f(x) = ax2 + bx + c
that satisfies the given conditions. Solve the system using matrices.
f(−2) = −11, f(1) = −5, f(2) = −23

Answer 1

`f(x)=-2x^2-3x-9`

Explanation:

Let
`f(x)=ax^2+bx+c` be the quadratic function.

`f(-2)=-11` implies that
`a(-2)^2+b(-2)+c=-11`

`4a-2b+c=-11......(1)`

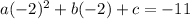
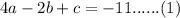
Similarly,
`f(1)=-5\implies a(1)^2+b(1)+c=-5\implies a+b=-5....(2)`

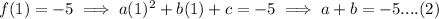
and
`f(2)=-23\implies a(2)^2+b(2)+c=-23\implies 4a+2b+c=-23...(3)`

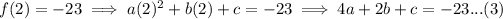
From equation 2,
`a=-b-5...(4)`

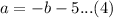
Put (4) into (1) to get:

`4(-b-5)-2b+c=-11\implies -6b+c=9....(5)`

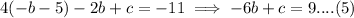
Put (4) in (3) to get:

`4(-b-5)+2b+c=-23\implies -2b+c=-3---(6)`

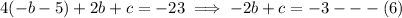
Subtract (6) from (5) to get:

`-4b=12`

`b=-3`

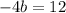
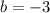
Put b=-3 in (4) to get:

a=--3-5=-2

Put b=-3 in to (6) to get:

-2(-3)+c=-3

6+c=-3

c=-6+-3=-9

Therefore the required equation is
`f(x)=-2x^2-3x-9`