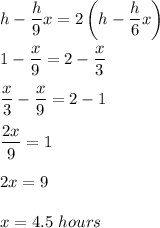Question

Two candles of equal length are lit at the same time. One candle takes 6 hours to burn out, and the other takes 9 hours to burn out. After how much time will the slower burning candle be exactly twice as long as the faster burning one?

Answer 1

4.5 hours

Explanation:

Two candles of equal length. Let h cm be the length of each candle.

1st candle:

It takes 6 hours to burn out, then
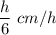`(h)/(6)\ cm/h` is the burning rate of the first candle.

2nd candle:

It takes 9 hours to burn out, then
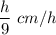`(h)/(9)\ cm/h` is the burning rate of the second candle.

In x hours, the first candle is
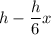`h-(h)/(6)x` cm long and the second candle is
`h-(h)/(9)x` cm long.

The slower burning candle (the second candle) will be exactly twice as long as the faster burning candle (the first candle) in

`h-(h)/(9)x=2\left(h-(h)/(6)x\right)\\ \\1-(x)/(9)=2-(x)/(3)\\ \\(x)/(3)-(x)/(9)=2-1\\ \\(2x)/(9)=1\\ \\2x=9\\ \\x=4.5\ hours`