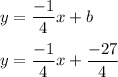Question

Find an equation of the line that passes through the points. (Let x be the independent variable and y be the dependent variable.)

(−3, −6) and (5, −8)

Answer 1

`y = (-1)/(4)x + (-27)/(4)`

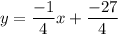
Explanation:

The equation of a line is:

y = mx + b

Where:

m = slope

b = y-intercept

First thing we need to do is solve for the slope. The slope formula is:

`m = (y_2-y_1)/(x_2-x_1)`

Where:

x₁ = x-coordinate of the first point

x₂ = x-coordinate of the second point

y₁ = y-coordinate of the first point

y₂ = y-coordinate of the second point

We are given the following points:

Point 1: (-3, -6)

Point 2: (5, -8)

So let's plug in our coordinates into the slope formula:

`m = (y_2-y_1)/(x_2-x_1)\\\\ =((-8)-(-6))/(5-(-3))\\\\ =(-2)/(8)\\\\ =(-1)/(4)`

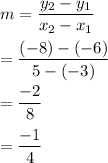
So we have our new equation of this line:

`y = (-1)/(4)x + b`

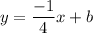
What do we do then about the y-intercept?

Our points will help us out by plugging them in our equation, so we can solve for our y-intercept (b).

Let's do both to show that it would be the same:

Point 1 (-3, -6)

`y = (-1)/(4)x + b\\\\-6 = (-1)/(4)(-3) + b\\\\-6 = (3)/(4) + b\\\\-6 = (3)/(4) + b\\\\subtract (3)/(4)\;from\;both\;sides\;of\;the\;equation\\\\-6- (3)/(4)= (3)/(4)- (3)/(4)+b\\\\\\(-24-3)/(4)=0+b\\\\\\-(27)/(4) = b`

Point 2: (5, -8)

`y = (-1)/(4)x + b\\\\-8 = (-1)/(4)(5) + b\\\\-8 = (-5)/(4) + b\\\\-8 = (-5)/(4) + b\\\\subtract (-5)/(4)\;from\;both\;sides\;of\;the\;equation\\\\-8- (-5)/(4)= (-5)/(4)- (-5)/(4)+b\\\\\\(-32-(-5))/(4)=0+b\\\\\\(-27)/(4) = b`

Now that we have b, we can insert that into the equation of the line:

`y = (-1)/(4)x + b\\\\y = (-1)/(4)x + (-27)/(4)`