Question

A golfer is on the edge of a 12.5 m bluff overlooking the 18th hole which is located 60 m from the base of the bluff. She launches a horizontal shot that lands in the hole on the fly. The gallery erupts in cheers.

Answer 1

The ball impact velocity i.e(velocity right before landing) is 6.359 m/s

Explanation:

This problem is related to parabolic motion and can be solved by the following equations:

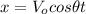`x=V_(o)cos \theta t`----------------------(1)

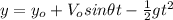`y=y_(o)+V_(o) sin \theta t - (1)/(2)gt^(2)`---------(2)

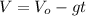`V=V_(o)-gt` ----------------------- (3)

Where:

x = m is the horizontal distance travelled by the golf ball

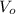`V_(o)` is the golf ball's initial velocity

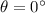`\theta=0\°` is the angle (it was a horizontal shot)

t is the time

y is the final height of the ball

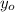`y_(o)` is the initial height of the ball

g is the acceleration due gravity

V is the final velocity of the ball

Step 1: finding t

Let use the equation(2)

`t=\sqrt{(2 y_(o))/(g)}`

`t=\sqrt{(2 (12.5 m))/(9.8 m/s^(2))}`

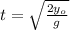
`t=1.597`s

Substituting (6) in (1):

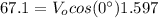`67.1 =V_(o) cos(0\°) 1.597`-------------------(4)

Step 2: Finding
`V_(o)`:

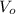From equation(4)

`67.1 =V_(o)(1) 1.597`

`V_0 = (6.71)/(1.597)`

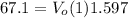
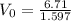
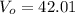`V_(o)=42.01` m/s (8)

Substituting
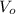`V_(o)` in (3):

`V=42.01 -(9.8)(1.597)`

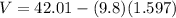
v =42 .01 - 15.3566

V=26.359 m/s