Question

Identify the equation of the circle that has its center at (10, 24) and passes through the origin.

A. (x−10)2+(y−24)2=676
B. (x−10)2+(y−24)2=576
C. (x+10)2+(y+24)2=676
D. (x+10)2+(y+24)2=576

Answer 1

A ) The Equation of the circle (x−10)2+(y−24)2=676

Explanation:

step1:-

The equation of the circle whose center is (a,b) and radius r is

`(x-a)^(2) +(y-b)^(2) =r^(2)`

`(x-10)^(2)+(y-24)^(2)  =676`

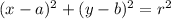
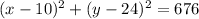
in this circle equation centre is (g,f) = (10,24)

and formula of radius of a circle is

r =
`\sqrt{g^(2)+f^(2) -c }`

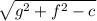
Step2:-

The Equation of the circle (x−10)^2+(y−24)^2=676