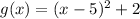Answer: Last option.
Explanation:
The complete question is: "What is the equation of the translated function,
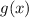 if
if
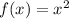 ?
?
The missing graph is attached.
Below are shown some transformations for a function
 :
:
1. If
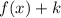 the function is translated "k" units up.
the function is translated "k" units up.
2. If
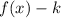 the function is translated "k" units down.
the function is translated "k" units down.
3. If
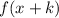 the function is translated "k" units to the left.
the function is translated "k" units to the left.
4. If
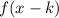 the function is translated "k" units to the right.
the function is translated "k" units to the right.
In this case, you can observe in the graph that the vertex of the parabola (function
 ) is at the following point:
) is at the following point:
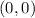
And the vertex of the translated parabola (function
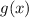 ) is at this point:
) is at this point:
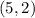
Therefore, based on the transformations explained before, you can identify that the function
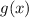 is obtained by translating the function
is obtained by translating the function
 5 units to the right and 2 units up.
5 units to the right and 2 units up.
Then, the equation of the function
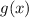 is:
is: