Question

A man is standing at a radar base and observes an unidentified plane at an altitude 6000m flying towards the radar base at an angle of elevation 300. After exactly one minute, the radar sweep reveals that the plane is now at an angle of elevation 600 maintaining the same altitude. What is the speed in m/s of the plane?

Answer 1

The speed in of the plane is 115.47 m/sec

Explanation:

Given:

Height at which the plane is flying = 6000 m

Angle of elevation at the radar base = 30 Degrees

Angle of elevation at the radar base after one minute = 60 Degrees

To Find:

The Speed of the plane in meter per second = ?

Solution:

Let us use the tangent of the angle to find the distance (d) to a point directly below plane:

when the angle is 30 degrees

`tan(30) = (6000)/(d1)`

`d1 = (6000)/(tan(30))`

`d1 = (6000)/(0.577)`

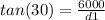
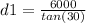
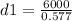
d1 = 10392.3 meters

when the angle is 60 degrees

`tan(60) = (6000)/(d2)`

`d2 = (6000)/(tan(60))`

`d2 = (6000)/(1.732)\\`

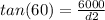
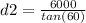
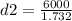
d2 = 3464.1 meters

distance travelled by aircraft in 1 min is

=>d1 - d2

=>0392.3 - 3464.1

= 6928.2 m/min

Now converting to m/sec

=>
`(6928.2)/(60)`

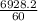
=>115.47 m/sec