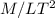Answer:
Step-by-step explanation:
Young's modulus is basically the ability of an object to resist change in its length when undergoes a tension or compression. It is a mechanical property of an object.
Now the formula for young's modulus or the modulus of elasticity is:
Young's modulus = Stress/Strain
As we know, strain is a dimensionless quantity, because it is a change in dimension divided by the original dimension, whereas stress has the same dimensions as pressure. Stress is
Stress = Force/Area
Now
Force = ma,
Where m = mass
a = acceleration
So, Stress = (ma)/Area
Acceleration = Velocity/Time
and Velocity = Distance/Time
So Acceleration = (Distance/Time)/Time
Now, what we have to understand here, is the basic dimensions are
M = mass
L = Length (or distance)
T = Time
So, by putting values for dimensions of stress
Stress (Dimensions) = Force/Area
Since Area = (meter)^2
Stress (Dimensions) = Force/L^2
substituting values for force
Stress (Dimensions) = ma/L^2
For mass dimension is M
Stress (Dimensions) = Ma/L^2
for acceleration, dimensions are L/T^2
Stress (Dimensions) = M(L/T^2)/L^2
by simplifying:
Stress (Dimensions) =
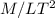
As we know that dimensions for Young's modulus will be same as the dimensions for Stress, So
Young's Modulus (Dimensions) =