Question

A tree with a height of 4m casts a shadow 15 m long on the ground. How high is another tree that casts a shadow which is 20 m long? Use the words similar, corresponding, or proportion to explain your work.

Answer 1

`\boxed{h=5.33\; m}`

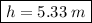
Explanation:

The 4m tree casts a shadow of 15m

Let h be the height of the tree and l, the shadow length

`(h)/(l) = (4)/(15)\\\\\\`

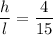
The length of the shadow is proportional to the height of the tree

For the tree of unknown height h and l = 20, this ratio must be the same.

`(h)/(20) = (4)/(15)\\\\`

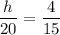
Multiply both sides by 20

`(h)/(20) \cdot 20 = (4)/(15) \cdot 20\\\\h = (16)/(3)= 5.33\;m\\`
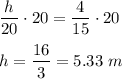
The length of the shadow is proportional to the height of the tree