Answer:
10%
Explanation:
Given: CP of lemon is $600.
3/4 of lemon sold at 20% loss
Remaining lemon at 20% gain.
Considering the quantity of lemon remain constant.
Cost price of 3/4 of lemon=
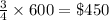
As given, 3/4 of lemon sold at 20% loss.
∴ Selling price of
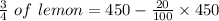
Selling price=
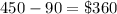
Hence, selling price of 3/4 lemon is $360.
Now, the cost price of remaining lemon
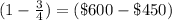
∴ The cost price of
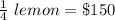
As given, remaining
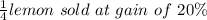
∴ Selling price of
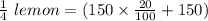
Selling price of
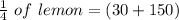
Hence, selling price of 1/4 lemon is $180
Loss\profit percent=
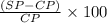
∴ Loss\profit percent=
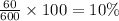
Hence, the loss percentage is 10%