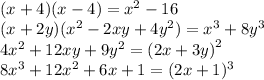Question

Drag the tiles to the correct boxes to complete the pairs.

Match each expression to its equivalent form.
Tiles
(x + 4)(x − 4)
(x + 2y)(x^2 − 2xy + 4y^2)
4x^2 + 12xy + 9y^2
8x^3 + 12x^2 + 6x + 1
Pairs
x^2 − 16

(2x + 1)^3

(2x + 3y)^2

x^3 + 8y^3

Answer 1

`(x + 4)(x-4)=x^2-16\\(x + 2y)(x^2-2xy + 4y^2)=x^3+ 8y^3\\4x^2 + 12xy + 9y^2=\left (2x+3y \right )^2\\8x^3 + 12x^2 + 6x + 1=(2x+1)^3`

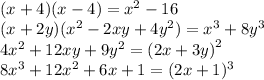
Explanation:

Algebraic Operations

Performing some basic algebraic operations we can transform expressions into others which could be more convenient to handle. For example, a polynomial can be factored for future simplifications or conclusions about its roots.

We have the following expressions and its operations to make them look like their equivalents

1.

`(x + 4)(x-4)`

We use the notable or special product to simplify:

`(x + 4)(x-4)=x^2-16`

2.

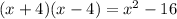
`(x + 2y)(x^2-2xy + 4y^2)`

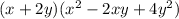
Performing the indicated products

`(x + 2y)(x^2-2xy + 4y^2)=x^3-2x^2y + 4xy^2+2yx^2-4xy^2 + 8y^3`

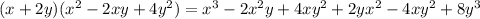
Simplifying

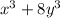
`x^3+ 8y^3`

3.

`4x^2 + 12xy + 9y^2`

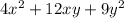
This is the square of a binomial. We find the square root of the first and last terms, then we test the second to be double of their product

`√(4x^2)=2x`

`√(9y^2)=3y`

`2(2x)(3y)=12xy`

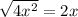
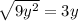
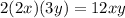
Since all the terms are correct, we can express it like

`\left (2x+3y \right )^2`

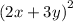
4.

`8x^3 + 12x^2 + 6x + 1`

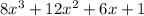
This is the cube of a binomial. Let's find the cubic root of the first and last term

`\sqrt[3]{8x^3}=2x`

`\sqrt[3]{1}=1`

The binomial is (2x+1). To prove it's correct, let's expand

`(2x+1)^3=8x^3 + 12x^2 + 6x + 1`

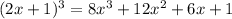
Thus, the expressions must be matched like this

`(x + 4)(x-4)=x^2-16\\(x + 2y)(x^2-2xy + 4y^2)=x^3+ 8y^3\\4x^2 + 12xy + 9y^2=\left (2x+3y \right )^2\\8x^3 + 12x^2 + 6x + 1=(2x+1)^3`