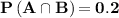Question

The sample space of a random experiment is {a b, , c, ,} d e with probabilities 0.1, 0.1, 0.2, 0.4, and 0.2, respectively. Let A denote the event {abc ,,}, and let B denote the event {cde , ,}. Determine the following:a. P(A)

b. P(B)
c. P(A’)
d. P(AUB)
e. P(AnB)

Answer 1

Explanation:

The concept of intersection and union of the events is used to solve this problem. The intersection of two events is the set of sample observations formed by the common sample points from the two events. The union of two events is the set formed by taking unique observations from the sample points constituting both the events.

Complementary events: If an event A is defined, then complement of event A is not occurring of event A.

Event: The collection or the set of outcomes in an experiment is called as an event.

Complementary events: If an event A is defined, then complement of event A is not occurring of event A.

Union of two events: The set of the outcomes that belong to either the two events or any of the two events is called as union of two events. Union of two events is denoted by (OR) or (u)

Intersection of two events: The set of the outcomes that belong to both the two events is called as intersection of two events. Intersection of the two events is denoted by (AND) or (∩)

(a)

The sample space of a random experiment is,

`S = \left\{ {a,b,c,d,e} \right\}</p><p>`

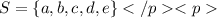
And,
`P\left( a \right) = 0.1,{\rm{ }}P\left( b \right) = 0.1,{\rm{ }}P\left( c \right) = 0.2,{\rm{ }}P\left( d \right) = 0.4,{\rm{ }}P\left( e \right) = 0.2`

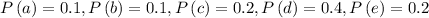
Let A be the event
`\left\{ {a,b,c} \right\}`

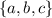
Now, calculate
`P\left( A \right)`

`\begin{array}{c}\\P\left( A \right) = P\left\{ {a,b,c} \right\}\\\\ = P\left( a \right) + P\left( b \right) + P\left( c \right)\\\\ = 0.1 + 0.1 + 0.2\\\\ = 0.4\\\end{array}`

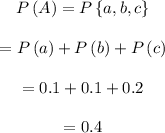
The probability of event
`{\bf{A = }}\left\{ {{\bf{a,b,c}}} \right\}A={a,b,c} is {\bf{P}}\left( {\bf{A}} \right){\bf{ = 0}}{\bf{.4}}`

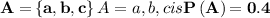
​b)

The sample space of a random experiment is,

`S = \left\{ {a,b,c,d,e} \right\}`

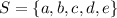
And,
`P\left( a \right) = 0.1,{\rm{ }}P\left( b \right) = 0.1,{\rm{ }}P\left( c \right) = 0.2,{\rm{ }}P\left( d \right) = 0.4,{\rm{ }}P\left( e \right) = 0.2`

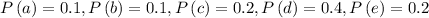
Let B be the event
`\left\{ {c,d,e} \right\}`

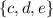
Now, calculate
`P\left( B \right)`

`\begin{array}{c}\\P\left( B \right) = P\left\{ {c,d,e} \right\}\\\\ = P\left( c \right) + P\left( d \right) + P\left( e \right)\\\\ = 0.2 + 0.4 + 0.2\\\\ = 0.8\\\end{array}`

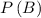
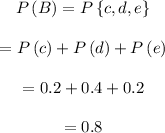
The probability of event
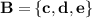`{\bf{B = }}\left\{ {{\bf{c}},{\bf{d,e}}} \right\}` is
`{\bf{P}}\left( {\bf{B}} \right){\bf{ = 0}}{\bf{.8}}`

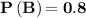
​(c)

From part (a), the probability event A is,
`P\left( A \right) = 0.4`

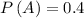
Then, the probability of event
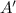`A'` is,

`\begin{array}{c}\\P\left( {A'} \right) = 1 - P\left( A \right)\\\\ = 1 - 0.4\\\\ = 0.6\\\end{array}`

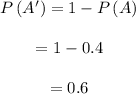
The probability of event
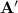`{\bf{A'}}` is
`{\bf{P}}\left( {{\bf{A'}}} \right){\bf{ = 0}}{\bf{.6}}`

d)

The sample space of a random experiment is,

`S = \left\{ {a,b,c,d,e} \right\}`

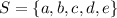
And,
`P\left( a \right) = 0.1,{\rm{ }}P\left( b \right) = 0.1,{\rm{ }}P\left( c \right) = 0.2,{\rm{ }}P\left( d \right) = 0.4,{\rm{ }}P\left( e \right) = 0.2`

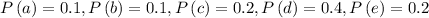
Let A be the event
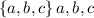`\left\{ {a,b,c} \right\}{a,b,c}` . Let B be the event
`\left\{ {c,d,e} \right\}`

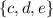
Checking the sample points in the entire sample space, find that the collection of sample points in the union of A and B.

`\begin{array}{c}\\A \cup B = \left\{ {a,b,c} \right\} \cup \left\{ {c,d,e} \right\}\\\\ = \left\{ {a,b,c,d,e} \right\}\\\end{array}`

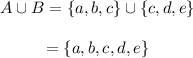
Now, calculate
`P\left( {A \cup B} \right)`

`\begin{array}{c}\\P\left( {A \cup B} \right) = P\left\{ {a,b,c,d,e} \right\}\\\\ = P\left( a \right) + P\left( b \right) + P\left( c \right) + P\left( d \right) + P\left( e \right)\\\\ = 0.1 + 0.1 + 0.2 + 0.4 + 0.2\\\\ = 1\\\end{array}`

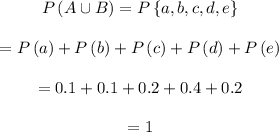
The probability of event
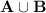`{\bf{A}} \cup {\bf{B}}` is
`{\bf{P}}\left( {{\bf{A}} \cup {\bf{B}}} \right){\bf{ = 1}}`

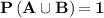
(e)

The sample space of a random experiment is,

`S = \left\{ {a,b,c,d,e} \right\}`

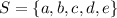
And,
`P\left( a \right) = 0.1,{\rm{ }}P\left( b \right) = 0.1,{\rm{ }}P\left( c \right) = 0.2,{\rm{ }}P\left( d \right) = 0.4,{\rm{ }}P\left( e \right) = 0.2`

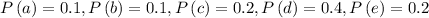
Let A be the event
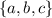`\left\{ {a,b,c} \right\}`. Let B be the event
`\left\{ {c,d,e} \right\}`

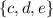
Check the sample points in the entire sample space, to find that the collection of sample points in both events A and B.

`\begin{array}{c}\\A \cap B = \left\{ {a,b,c} \right\} \cap \left\{ {c,d,e} \right\}\\\\ = \left\{ c \right\}\\\end{array}`

Now, calculate
`P\left( {A \cap B} \right)`

`\begin{array}{c}\\P\left( {A \cap B} \right) = P\left( c \right)\\\\ = 0.2\\\end{array}`

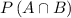
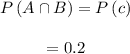
The probability of event
`{\bf{A}} \cap {\bf{B}}` is
`{\bf{P}}\left( {{\bf{A}} \cap {\bf{B}}} \right){\bf{ = 0}}{\bf{.2}}`