Question

The roots of a quadratic equation ax2+bx+c=0 are 1+i 5 and 1−i 5 . Find possible values of a, b and c.

Answer 1

Explanation:

If the roots are 1 + 5i and 1 - 5i, then you need the factors that result from those roots. They are (x - 1 + 5i) and (x - 1 - 5i). Now what you do with those is FOIL them out. Doing that gives you the following:

`x^2-x+5ix-x+1-5i-5ix+5i-25i^2` (what a mess, huh?)

The good thing is that several of those terms cancel each other out. +5ix cancels out the -5ix; -5i cancels out the 5i; and the 2 -x terms combine to -2x. That leaves you with:

`x^2-2x-25i^2`

Obviously you're in the section in math that deals with complex (imaginary) numbers so you should know that i-squared is equal to -1. Making that replacement:

`x^2-2x+25`

a = 1, b = -2, c = 25

Answer 2

`a\\eq 0`,
`b=-2a, c=6a`

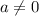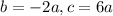
Explanation:

Use Vieta's theorem:

`(-b)/(a) = 1+i√(5)+1-i√(5) = 2`

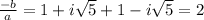
so b=-2a

`(c)/(a) = (1+i√(5))(1-i√(5) ) = 1+5 = 6`

so c = 6a

Coefficient a can technically be any number except 0, because if we look at the vertex form of the ax2+bx+c=0 equation, which is: a(x-r)(x-v)=0 (r and v being the roots), we can see that any value of a would end up with the same resulting quadratic. (we're just multiplying the whole equation by one number).

However, a can't equal zero because if we set a as zero in ax^2+bx+c=0, this equation wouldn't be a parabola anymore. There would be no x^2, and the the graph would just be a linear line.

So if we combine the two cases of a being any number and it not being zero, the result is
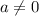`a\\eq 0`.