Question

A large city newspaper periodically reports the mean cost of dinner for two people at restaurants in the city. The newspaper staff will collect data from a random sample of restaurants in the city and estimate the mean price using a 90 percent confidence interval. In past years, the standard deviation has always been very close to $35. Assuming that the population standard deviation is $35, which of the following is the minimum sample size needed to obtain a margin of error of no more than $5 ?A) 90

B) 112
C) 133
D)147

Answer 1

Answer: C) 133

Explanation:

The formula to find the sample size is given by :-

`n=((z^*\cdot\sigma)/(E))^2`

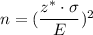
, where z* = Critical z-value

`\sigma` = Population standard deviation for prior study.

E= Margin of error.

As per given , we have

`\sigma=$35`

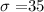
E= 5

The critical z-value for 90% confidence level is 1.645.

Substitute al;l the value sin the above formula , we get

`n=((1.645* 35)/(5))^2`

`n=((57.575)/(5))^2`

`n=(11.515)^2`

`n=132.595225\approx133`

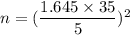
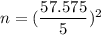
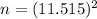
Hence, the minimum sample size needed is 133.

Thus , the correct answer is : C) 133