Question

Going to the prom Tonya wants to estimate what proportion of her school’s seniors plan to attend the prom. She interviews an SRS of 50 of the 750 seniors in her school and finds that 36 plan to go to the prom.

(a) Identify the population and parameter of interest.

(b) Check conditions for constructing a confidence interval for the parameter.

(c) Construct a 90% confidence interval for p. Show your method.

(d) Interpret the interval in context.

Answer 1

The student wants to estimate the proportion of seniors who plan to attend prom in their school. A 90% confidence interval is constructed using the sample data. The interpretation of the interval is also provided.

Step-by-step explanation:

(a) The population of interest is the entire senior class of Tonya's school, which consists of 750 seniors. The parameter of interest is the proportion of seniors who plan to attend the prom.

(b) To construct a confidence interval for the proportion, we need to check the conditions:

1. The sample was selected randomly, so the students Tonya interviewed can be considered a simple random sample (SRS).
2. The sample size is large enough, with 50 students, so we can assume independence and normality.
3. We can assume that the proportion of seniors who plan to attend the prom is consistent throughout the population (no systematic bias or outliers).

(c) To construct a 90% confidence interval, we can use the following formula:

`CI = p +/- z * sqrt((p * (1-p)) / n)`

Where:

p is the sample proportion (36/50)

z is the critical value corresponding to a 90% confidence level (1.645 for a two-tailed test)

n is the sample size (50)

By substituting the values into the formula, we can calculate the confidence interval.

(d) The confidence interval represents the range of plausible values for the proportion of seniors who plan to attend the prom. In this case, the 90% confidence interval would be interpreted as: We are 90% confident that the true proportion of seniors who plan to attend the prom is between [lower bound] and [upper bound].

Answer 2

We are 90% confident that for large samples randomly drawn from 750 seniors the proportion of seniors who plan to go the prom will fall within this interval

Step-by-step explanation:

Given that going to the prom Tonya wants to estimate what proportion of her school’s seniors plan to attend the prom. She interviews an SRS of 50 of the 750 seniors in her school and finds that 36 plan to go to the prom.

a) Here population of interest is all the 750 seniors in her school and parameter of interest is the proportion of seniors who plan to go to the prom.

b) The conditions for constructing confidence interval are

i) Sample should be strictly drawn at random. So ensure that 50 students are taken without any bias and at random

ii) Whether sample size is adequate to represent the population. Here 50 is a good number more than 30 and hence sufficient.

c) For 90% confidence we use z critical as 1.645

Sample proportion P =
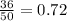`(36)/(50) =0.72`Q= 1-P=0.28

n = 50

Std error of sample proporiton P =
`\sqrt{(PQ)/(n) } \\=\sqrt{(0.72*0.28)/(50) } \\=0.0635`

Margin of error = 1.645 *0.0635 =0.1045

Confidence interval = P±Margin of error

= (0.6155, 0.8245)

d) We are 90% confident that for large samples randomly drawn from 750 seniors the proportion of seniors who plan to go the prom will fall within this interval