Question

Simplify the expression and rewrite in rational exponent form.

Answer 1

`4 x^{(11)/(10)} \cdot y^{(17)/(3)}`

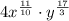
Explanation:

The given expression:
`4 \sqrt[5]{x^(3)} \cdot y^(4) \cdot √(x) \cdot \sqrt[3]{y^(5)}`

Step 1: Change radical to fractional exponent.

Formula for fractional exponent:
`\sqrt[n]{a}=a^{(1)/(n)}`

The power to which the base is raised becomes the numerator and the root becomes the denominator.

`\Rightarrow 4 x^{(3)/(5)} \cdot y^(4) \cdot x^{(1)/(2)} \cdot y^{(5)/(3)}`

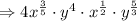
Step 2: Apply law of exponent for a product
`a^(m) * a^(n)=a^(m+n)`

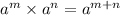
Multiply powers with same base.

`\Rightarrow 4 x^{(3)/(5)+(1)/(2)} \cdot y^{4+(5)/(8)}`

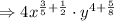
Take LCM for the fractions in the power.

`\Rightarrow 4 x^{(6)/(10)+(5)/(10)} \cdot y^{(12)/(3)+(5)/(3)}`

`\Rightarrow 4 x^{(11)/(10)} \cdot y^{(17)/(3)}`

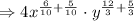
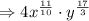
Hence the simplified form of
`4 \sqrt[5]{x^(3)} \cdot y^(4) \cdot √(x) \cdot \sqrt[3]{y^(5)} \text { is } 4 x^{(11)/(10)} \cdot y^{(17)/(3)}`.