Question

The question is: The IQs of 9 randomly selected people are recorded. Let Y(bar) denote their average.

Assuming the distribution from which the Yi's were drawn is normal with a mean of 100 and a standard deviation of 16, what is the probability that Y(bar) will exceed 103?

What is the probability that any arbitrary Yi will exceed 103?

What is the probability that exactly 3 of the Yi's will exceed 103?

Answer 1

a.
`0.42465\approx 42.5\%`

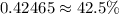
b. 0.23

Explanation:

We have been given that the the distribution from which the Yi's were drawn is normal with a mean of 100 and a standard deviation of 16.

(a) We are asked to find the probability that any arbitrary Yi will exceed 103.

Let us calculate z-score corresponding to 103 using z-score formula.

`z=(x-\mu)/(\sigma)`

`z=(103-100)/(16)`

`z=(3)/(16)`

`z=0.1875`

`z\approx 0.19`

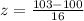
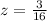
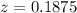
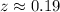
Now, we need to find
`p(z>0.19)`.

`P(z>0.19)=1-)(z<0.19)`

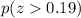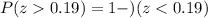
Using normal distribution table, we will get:

`P(z>0.19)=1-0.57535`

`P(z>0.19)=0.42465`

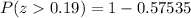
Therefore, the probability, that any arbitrary Yi will exceed 103, is 0.42465 or 42.5%.

(b) To find the probability that exactly 3 of the Yi's will exceed 103, we will use binomial probability formula.

`_nC_r\cdot P^r\cdot (1-P)^(n-r)`

For the given scenario
`P=0.42465`,
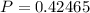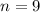`n=9` and
`r=3`.

`(9!)/(3!(9-3)!)\cdot (0.42465)^(3)\cdot (1-0.42465)^(9-3)`

`(9*8*7*6!)/(3*2*6!)\cdot (0.42465)^(3)\cdot (0.57535)^(6)`

`3*4*7\cdot 0.076576124894625\cdot 0.0362737708038501`

`84\cdot 0.076576124894625\cdot 0.0362737708038501`

`0.23332720349186\approx 0.23`

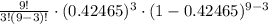
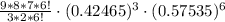
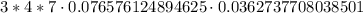
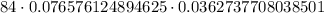
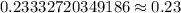
Therefore, the probability, that exactly 3 of the Yi's will exceed 103, is approximately 0.23 or 23%.