Question

You have 40 inches of wire and you want to use two sections of it to form the outlines of a square and a circle. How much of it should be used for the square, and how much for the circle, so that there is a minimum amount of area for the combined shapes?

Answer 1

22.404 inches of the wire should be used for square

17.596 inches of the wire should be used for the circle.

Explanation:

We're forming one square and one circle from a 40 inch long wire.

Hence we know that the sum of the perimeters(P) of the two shapes will be 40.

`P_\text{square}+P_\text{circle}=40`

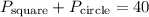
let,

• 
  `x` be the side-length of the square

• 
  `r` be the radius of the circle.

`4x+2\pi r=40`

It is also stated that the combined area of both shapes should be minimum.

Hence, we can formulate the sum of the areas(A) similarly to how we did for perimeters.

`A_\text{square}+A_\text{circle}=y`

`y` is the combined area

`y=x^2+\pi r^2`

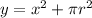
this is a function y(x,r). In order to find the minimum combined area, we need to differentiate the function. But first we need to replace one of the variables 'x' or 'r' so that the function 'y' only has one variable.

`r=(40-4x)/(2\pi)`

we can substitute this in y

`y=x^2+\pi \left((40-4x)/(2\pi)\right)^2\\y=x^2+(1)/(4\pi)(40-4x)^2\\(dy)/(dx)=2x+(2)(1)/(4\pi)(40-4x)(-4)\\(dy)/(dx)=2x-(2)/(\pi)(40-4x)\\`

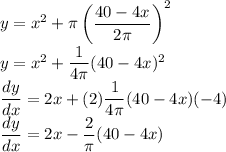
now substitute
`(dy)/(dx)=0`

`0=2x-(2)/(\pi)(40-4x)\\0=(2\pi x-2(40-4x))/(\pi)\\0=\pi x-40+4x\\0=x(\pi+4)-40\\x=(40)/(\pi+4)\approx5.601`

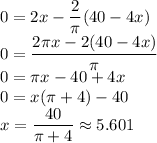
we can use this to find 'r'.

`r=(40-4x)/(2\pi)\\2\pi r =40-4\left((40)/(\pi+4)\right)\\2\pi r = (40\pi+160-160)/(\pi+4)\\r=(20)/(\pi+4)\approx2.80`

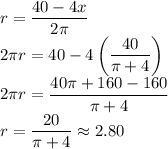
these are the dimensions of the two shapes for which the combined areas will be minimum.

we can find how much of the wire segments will be used for each of the shapes.

`P_\text{square}+P_\text{circle}=40`

`4x+2\pi r=40`

`4\left((40)/(\pi+4)\right)+2\pi \left((20)/(\pi+4)\right)=40`

`22.404+17.596=40`

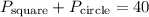
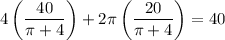
22.404 inches of the wire should be used for square

17.596 inches of the wire should be used for the circle.